Примеры на метод вариации произвольной постоянной. Метод лагранжа вариации произвольных постоянных
Лекция 44. Линейные неоднородные уравнения второго порядка. Метод вариации произвольных постоянных. Линейные неоднородные уравнения второго порядка с постоянными коэффициентами. (специальная правая часть).
Социальные преобразования. Государство и церковь.
Социальная политика большевиков во многом диктовалась их классовым подходом. Декретом от 10 ноября 1917 г. уничтожена сословная система, отменены дореволюционные чины, титулы и награды. Установлена выборность судей; проведена секуляризация гражданских состояний. Установлено бесплатное образование и медицинское обслуживание (декрет от 31 октября 1918 г.). Женщины уравнивались в правах с мужчинами (декреты от 16 и 18 декабря 1917 г.). Декрет о браке вводил институт гражданского брака.
Декретом СНК от 20 января 1918 года церковь отделена от государства и от системы образования. Большая часть церковного имущества конфискована. Патриарх Московский и всея Руси Тихон (избран 5 ноября 1917 года) 19 января 1918 года предал анафеме Советскую власть и призвал к борьбе против большевиков.
Рассмотрим линейное неоднородное уравнение второго порядка
Структура общего решения такого уравнения определяется следующей теоремой:
Теорема 1. Общее решение неоднородного уравнения (1) представляется как сумма какого-нибудь частного решения этого уравнения и общего решения соответствующего однородного уравнения
![]() (2)
(2)
Доказательство . Нужно доказать, что сумма
есть общее решение уравнения (1). Докажем сначала, что функция (3) есть решение уравнения (1).
Подставляя сумму в уравнение (1) вместо у , будем иметь
Так как есть решение уравнение (2), то выражение, стоящее в первых скобках, тождественно равно нулю. Так как есть решение уравнения (1), то выражение, стоящее во вторых скобках, равно f(x) . Следовательно, равенство (4) является тождеством. Таким образом, первая часть теоремы доказана.
Докажем второе утверждение: выражение (3) есть общее решение уравнения (1). Мы должны доказать, что входящие в это выражение произвольные постоянные можно подобрать так, чтобы удовлетворялись начальные условия:
![]() (5)
(5)
каковы бы ни были числа х 0 , y 0 и (лишь бы х 0 было взято из той области, где функции а 1 , а 2 и f(x) непрерывны).
Заметив, что можно представить в форме ![]() . Тогда на основании условий (5) будем иметь
. Тогда на основании условий (5) будем иметь

Решим эту систему и определим С 1 и С 2 . Перепишем систему в виде:
 (6)
(6)
Заметим, что определитель этой системы есть определитель Вронского для функций у 1 и у 2 в точке х=х 0 . Так как эти функции по условию линейно независимы, то определитель Вронского не равен нулю; следовательно система (6) имеет определенное решение С 1 и С 2 , т.е. существуют такие значения С 1 и С 2 , при которых формула (3) определяет решение уравнения (1), удовлетворяющее данным начальным условиям. Что и требовалось доказать.
Перейдем к общему методу нахождения частных решений неоднородного уравнения.
Напишем общее решение однородного уравнения (2)
![]() . (7)
. (7)
Будем искать частное решение неоднородного уравнения (1) в форме (7), рассматривая С 1 и С 2 как некоторые пока неизвестные функции от х.
Продифференцируем равенство (7):
Подберем искомые функции С 1 и С 2 так, чтобы выполнялось равенство
![]() . (8)
. (8)
Если учесть это дополнительное условие, то первая производная примет вид
![]() .
.
Дифференцируя теперь это выражение, найдем :
Подставляя в уравнение (1), получим
Выражения, стоящие в первых двух скобках, обращаются в нуль, так как y 1 и y 2 – решения однородного уравнения. Следовательно, последнее равенство принимает вид
![]() . (9)
. (9)
Таким образом, функция (7) будет решением неоднородного уравнения (1) в том случае, если функции С 1 и С 2 удовлетворяют уравнениям (8) и (9). Составим систему уравнений из уравнений (8) и (9).

Так как определителем этой системы является определитель Вронского для линейно независимых решений y 1 и y 2 уравнения (2), то он не равен нулю. Следовательно, решая систему, мы найдем как определенные функции от х .
Рассмотрим теперь линейное неоднородное уравнение
. (2)
Пусть y 1 ,y 2 ,.., y n - фундаментальная система решений, а - общее решение соответствующего однородного уравнения L(y)=0 . Аналогично случаю уравнений первого порядка, будем искать решение уравнения (2) в виде
. (3)
Убедимся в том, что решение в таком виде существует. Для этого подставим функцию в уравнение. Для подстановки этой функции в уравнение найдём её производные. Первая производная равна
 . (4)
. (4)
При вычислении второй производной в правой части (4) появится четыре слагаемых, при вычислении третьей производной - восемь слагаемых и так далее. Поэтому, для удобства дальнейшего счёта, первое слагаемое в (4) полагают равным нулю. С учётом этого, вторая производная равна
 . (5)
. (5)
По тем же, что и раньше, соображениям, в (5) также полагаем первое слагаемое равным нулю. Наконец, n-я производная равна
 . (6)
. (6)
Подставляя полученные значения производных в исходное уравнение, имеем
 . (7)
. (7)
Второе слагаемое в (7) равно нулю, так как функции y j , j=1,2,..,n, являются решениями соответствующего однородного уравнения L(y)=0. Объединяя с предыдущим, получаем систему алгебраических уравнений для нахождения функций C" j (x)
 (8)
(8)
Определитель этой системы есть определитель Вронского фундаментальной системы решений y 1 ,y 2 ,..,y n соответствующего однородного уравнения L(y)=0 и поэтому не равен нулю. Следовательно, существует единственное решение системы (8). Найдя его, получим функции C" j (x), j=1,2,…,n, а, следовательно, и C j (x), j=1,2,…,n Подставляя эти значения в (3), получаем решение линейного неоднородного уравнения.
Изложенный метод называется методом вариации произвольной постоянной или методом Лагранжа.
Пример №1 . Найдём общее решение уравнения y"" + 4y" + 3y = 9e -3 x . Рассмотрим соответствующее однородное уравнение y"" + 4y" + 3y = 0. Корни его характеристического уравнения r 2 + 4r + 3 = 0 равны -1 и -3. Поэтому фундаментальная система решений однородного уравнения состоит из функций y 1 = e - x и y 2 = e -3 x . Решение неоднородного уравнения ищем в виде y = C 1 (x)e - x + C 2 (x)e -3 x . Для нахождения производных C" 1 , C" 2 составляем систему уравнений (8)

решая которую, находим , Интегрируя полученные функции, имеем
Окончательно получим
Пример №2
. Решить линейные дифференциальные уравнения второго порядка с постоянными коэффициентами методом вариации произвольных постоянных:
![]()
y(0) =1 + 3ln3
y’(0) = 10ln3
Решение:
Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям с постоянными коэффициентами.
Решение уравнения будем искать в виде y = e rx . Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами:
r 2 -6 r + 8 = 0
D = (-6) 2 - 4 1 8 = 4
Корни характеристического уравнения: r 1 = 4, r 2 = 2
Следовательно, фундаментальную систему решений составляют функции:
y 1 = e 4x , y 2 = e 2x
Общее решение однородного уравнения имеет вид:
![]()
Поиск частного решения методом вариации произвольной постоянной.
Для нахождения производных C" i составляем систему уравнений:
![]()
C" 1 (4e 4x) + C" 2 (2e 2x) = 4/(2+e -2x)
Выразим C" 1 из первого уравнения:
C" 1 = -c 2 e -2x
и подставим во второе. В итоге получаем:
C" 1 = 2/(e 2x +2e 4x)
C" 2 = -2e 2x /(e 2x +2e 4x)
Интегрируем полученные функции C" i:
C 1 = 2ln(e -2x +2) - e -2x + C * 1
C 2 = ln(2e 2x +1) – 2x+ C * 2
Поскольку ![]() , то записываем полученные выражения в виде:
, то записываем полученные выражения в виде:
C 1 = (2ln(e -2x +2) - e -2x + C * 1) e 4x = 2 e 4x ln(e -2x +2) - e 2x + C * 1 e 4x
C 2 = (ln(2e 2x +1) – 2x+ C * 2)e 2x = e 2x ln(2e 2x +1) – 2x e 2x + C * 2 e 2x
Таким образом, общее решение дифференциального уравнения имеет вид:
y = 2 e 4x ln(e -2x +2) - e 2x + C * 1 e 4x + e 2x ln(2e 2x +1) – 2x e 2x + C * 2 e 2x
или
y = 2 e 4x ln(e -2x +2) - e 2x + e 2x ln(2e 2x +1) – 2x e 2x + C * 1 e 4x + C * 2 e 2x
Найдем частное решение при условии:
y(0) =1 + 3ln3
y’(0) = 10ln3
Подставляя x = 0, в найденное уравнение, получим:
y(0) = 2 ln(3) - 1 + ln(3) + C * 1 + C * 2 = 3 ln(3) - 1 + C * 1 + C * 2 = 1 + 3ln3
Находим первую производную от полученного общего решения:
y’ = 2e 2x (2C 1 e 2x + C 2 -2x +4 e 2x ln(e -2x +2)+ ln(2e 2x +1)-2)
Подставляя x = 0, получим:
y’(0) = 2(2C 1 + C 2 +4 ln(3)+ ln(3)-2) = 4C 1 + 2C 2 +10 ln(3) -4 = 10ln3
Получаем систему из двух уравнений:
3 ln(3) - 1 + C * 1 + C * 2 = 1 + 3ln3
4C 1 + 2C 2 +10 ln(3) -4 = 10ln3
или
C * 1 + C * 2 = 2
4C 1 + 2C 2 = 4
или
C * 1 + C * 2 = 2
2C 1 + C 2 = 2
Откуда:
C 1 = 0, C * 2 = 2
Частное решение запишется как:
y = 2 e 4x ln(e -2x +2) - e 2x + e 2x ln(2e 2x +1) – 2x e 2x + 2 e 2x
Метод вариации произвольных постоянных
Метод вариации произвольных постоянных для построения решения линейного неоднородного дифференциального уравнения
a n (t )z (n ) (t ) + a n − 1 (t )z (n − 1) (t ) + ... + a 1 (t )z "(t ) + a 0 (t )z (t ) = f (t )
состоит в замене произвольных постоянных c k в общем решении
z (t ) = c 1 z 1 (t ) + c 2 z 2 (t ) + ... + c n z n (t )
соответствующего однородного уравнения
a n (t )z (n ) (t ) + a n − 1 (t )z (n − 1) (t ) + ... + a 1 (t )z "(t ) + a 0 (t )z (t ) = 0
на вспомогательные функции c k (t ) , производные которых удовлетворяют линейной алгебраической системе
Определителем системы (1) служит вронскиан функций z 1 ,z 2 ,...,z n , что обеспечивает её однозначную разрешимость относительно .
Если - первообразные для , взятые при фиксированных значениях постоянных интегрирования, то функция
является решением исходного линейного неоднородного дифференциального уравнения. Интегрирование неоднородного уравнения при наличии общего решения соответствующего однородного уравнения сводится, таким образом, к квадратурам .
Метод вариации произвольных постоянных для построения решений системы линейных дифференциальных уравнений в векторной нормальной форме
состоит в построении частного решения (1) в виде
где Z (t ) - базис решений соответствующего однородного уравнения, записанный в виде матрицы, а векторная функция , заменившая вектор произвольных постоянных, определена соотношением . Искомое частное решение (с нулевыми начальными значениями при t = t 0 имеет вид

Для системы с постоянными коэффициентами последнее выражение упрощается:

Матрица Z (t )Z − 1 (τ) называется матрицей Коши оператора L = A (t ) .
Внешние ссылки
- exponenta.ru - Теоретическая справка c примерами
Wikimedia Foundation . 2010 .
Рассмотрим линейное неоднородное дифференциальное уравнение первого порядка:
(1)
.
Существует три способа решения этого уравнения:
- метод вариации постоянной (Лагранжа).
Рассмотрим решение линейного дифференциального уравнения первого порядка методом Лагранжа.
Метод вариации постоянной (Лагранжа)
В методе вариации постоянной мы решаем уравнение в два этапа. На первом этапе мы упрощаем исходное уравнение и решаем однородное уравнение. На втором этапе мы заменим постоянную интегрирования, полученную на первой стадии решения, на функцию. После чего ищем общее решение исходного уравнения.
Рассмотрим уравнение:
(1)
Шаг 1 Решение однородного уравнения
Ищем решение однородного уравнения:
Это уравнение с разделяющимися переменными
Разделяем переменные - умножаем на dx
,
делим на y
:
Интегрируем:
Интеграл по y
- табличный :
Тогда
Потенцируем:
Заменим постоянную e C
на C
и уберем знак модуля, что сводится к умножению на постоянную ±1
,
которую включим в C
:
Шаг 2 Заменим постоянную C на функцию
Теперь заменим постоянную C
на функцию от x
:
C → u(x)
То есть, будем искать решение исходного уравнения (1)
в виде:
(2)
Находим производную.
По правилу дифференцирования сложной функции:
.
По правилу дифференцирования произведения:
.
Подставляем в исходное уравнение (1)
:
(1)
;
.
Два члена сокращаются:
;
.
Интегрируем:
.
Подставляем в (2)
:
.
В результате получаем общее решение линейного дифференциального уравнения первого порядка:
.
Пример решения линейного дифференциального уравнения первого порядка методом Лагранжа
Решить уравнение
Решение
Решаем однородное уравнение:
Разделяем переменные:
Умножим на :
Интегрируем:
Интегралы табличные :
Потенцируем:
Заменим постоянную e C
на C
и убираем знаки модуля:
Отсюда:
Заменим постоянную C
на функцию от x
:
C → u(x)
Находим производную:
.
Подставляем в исходное уравнение:
;
;
Или:
;
.
Интегрируем:
;
Решение уравнения:
.
Рассмотрим линейное неоднородное дифференциальное уравнение с постоянными коэффициентами произвольного n-го порядка:
(1)
.
Метод вариации постоянной, рассмотренный нами для уравнения первого порядка , также применим и для уравнений более высоких порядков.
Решение выполняется в два этапа. На первом этапе мы отбрасываем правую часть и решаем однородное уравнение. В результате получаем решение, содержащее n произвольных постоянных. На втором этапе мы варьируем постоянные. То есть мы считаем, что эти постоянные являются функциями от независимой переменной x и находим вид этих функций.
Хотя мы здесь рассматриваем уравнения с постоянными коэффициентами, но метод Лагранжа также применим и для решения любых линейных неоднородных уравнений . Для этого, однако, должна быть известна фундаментальная система решений однородного уравнения.
Шаг 1. Решение однородного уравнения
Как и в случае уравнений первого порядка, вначале мы ищем общее решение однородного уравнения, приравнивая правую неоднородную часть к нулю:
(2)
.
Общее решение такого уравнения имеет вид:
(3)
.
Здесь - произвольные постоянные; - n
линейно независимых решений однородного уравнения (2), которые образуют фундаментальную систему решений этого уравнения.
Шаг 2. Вариация постоянных - замена постоянных функциями
На втором этапе мы займемся вариацией постоянных. Другими словами, мы заменим постоянные на функции от независимой переменной x
:
.
То есть мы ищем решение исходного уравнения (1) в следующем виде:
(4)
.
Если мы подставим (4) в (1), то получим одно дифференциальное уравнение для n функций . При этом мы можем связать эти функции дополнительными уравнениями. Тогда получится n уравнений, из которых можно определить n функций . Дополнительные уравнения можно составить различными способами. Но мы это сделаем так, чтобы решение имело наиболее простой вид. Для этого, при дифференцировании, нужно приравнивать к нулю члены, содержащие производные от функций . Продемонстрируем это.
Чтобы подставить предполагаемое решение (4) в исходное уравнение (1), нам нужно найти производные первых n
порядков от функции, записанной в виде (4). Дифференцируем (4), применяя правила дифференцирования суммы
и произведения
:
.
Сгруппируем члены. Сначала выпишем члены с производными от ,
а затем - члены с производными от :
.
Наложим на функции первое условие:
(5.1)
.
Тогда выражение для первой производной по будет иметь более простой вид:
(6.1)
.
Тем же способом находим вторую производную:
.
Наложим на функции второе условие:
(5.2)
.
Тогда
(6.2)
.
И так далее. В дополнительных условиях, мы приравниваем члены, содержащие производные функций ,
к нулю.
Таким образом, если выбрать следующие дополнительные уравнения для функций :
(5.k)
,
то первые производных по будут иметь наиболее простой вид:
(6.k)
.
Здесь .
Находим n
-ю производную:
(6.n)
.
Подставляем в исходное уравнение (1):
(1)
;
.
Учтем, что все функции удовлетворяют уравнению (2):
.
Тогда сумма членов, содержащих дают нуль. В итоге получаем:
(7)
.
В результате мы получили систему линейных уравнений для производных :
(5.1)
;
(5.2)
;
(5.3)
;
. . . . . . .
(5.n-1)
;
(7′)
.
Решая эту систему, находим выражения для производных как функции от x
.
Интегрируя, получим:
.
Здесь - уже не зависящие от x
постоянные. Подставляя в (4), получаем общее решение исходного уравнения.
Заметим, что для определения величин производных мы нигде не использовали тот факт, что коэффициенты a i являются постоянными. Поэтому метод Лагранжа применим для решения любых линейных неоднородных уравнений , если известна фундаментальная система решений однородного уравнения (2).
Примеры
Решить уравнения методом вариации постоянных (Лагранжа).
-
 «Комплексный подход к работе учителя – логопеда и педагога – психолога с детьми, имеющими речевые нарушения Характеристика изменений в
образовательном процессе
«Комплексный подход к работе учителя – логопеда и педагога – психолога с детьми, имеющими речевые нарушения Характеристика изменений в
образовательном процессе
-
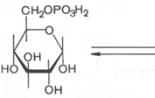 Бескислородное окисление глюкозы включает два этапа
Бескислородное окисление глюкозы включает два этапа
-
 Иисус навин кто он. Иисус сын навин. Вхождение в Землю Обетованную
Иисус навин кто он. Иисус сын навин. Вхождение в Землю Обетованную
-
 Что делать если заказ не пришел с eBay?
Что делать если заказ не пришел с eBay?










