Как определяется проекция вектора на координатные оси. Проекция вектора. Координатные оси. Проекция точки. Координаты точки на ось. Скалярные и векторные величины
По
физике
за 9 класс (И.К.Кикоин, А.К.Кикоин, 1999 год),
задача №5
к главе «ГЛАВА 1. ОБЩИЕ СВЕДЕНИЯ О ДВИЖЕНИИ
».
1. Что называют проекцией вектора на координатную ось?
1. Проекцией вектора а на координатную ось называют длину отрезка между проекциями начала и конца вектора а (перпендикулярами, опущенными из этих точек на ось) на эту координатную ось.
2. Как связан вектор перемещения тела с его координатами?
2. Проекции вектора перемещения s на оси координат равны изменению соответствующих координат тела.
3. Если координата точки с течением времени увеличивается, то какой знак имеет проекция вектора перемещения на координатную ось? А если она уменьшается?
3. Если координата точки с течением времени увеличивается, то проекция вектора перемещения на координатную ось будет положительной, т.к. в этом случае мы будем идти от проекции начала к проекции конца вектора по направлению самой оси.
Если координата точки с течением времени будет уменьшаться, то проекция вектора перемещения на координатную ось будет отрицательной, т.к. в этом случае мы будем идти от проекции начала к проекции конца вектора против направляющей самой оси.
4. Если вектор перемещения параллелен оси X, то чему равен модуль проекции вектора на эту ось? А модуль проекции этого же вектора на ось У?
4. Если вектор перемещения параллелен оси Х, то модуль проекции вектора на эту ось равен модулю самого вектора, а его проекция на ось Y равна нулю.
5. Определите знаки проекций на ось X векторов перемещения, изображенных на рисунке 22. Как при этих перемещениях изменяются координаты тела?
5. Во всех нижеследующих случаях координата Y тела не изменяется, а координата Х тела будет изменяться следующим образом:
a) s 1 ;
проекция вектора s 1 , на ось Х отрицательна и по модулю равна длине вектора s 1 . При таком перемещении координата Х тела уменьшится на длину вектора s 1 .
b) s 2 ;
проекция вектора s 2 на ось X положительна и равна по модулю длине вектора s 1 . При таком перемещении координата Х тела увеличится на длину вектора s 2 .
c) s 3 ;
проекция вектора s 3 на ось Х отрицательна и равна по модулю длине вектора s 3 . При таком перемещении координата Х тела уменьшится на длину вектора s 3 .
d) s 4 ;
проекция вектора s 4 на ось X положительна и равна по модулю длине вектора s 4 . При таком перемещении координата Х тела увеличится на длину вектора s 4 .
e) s 5 ;
проекция вектора s 5 на ось Х отрицательна и равна по модулю длине вектора s 5 . При таком перемещении координата Х тела уменьшится на длину вектора s 5 .
6. Если значение пройденного пути велико, то может ли модуль перемещения быть малым?
6. Может. Это связано с тем, что перемещение (вектор перемещения) является векторной величиной, т.е. представляет собой направленный отрезок прямой, соединяющий начальное положение тела с его последующими положениями. А конечное положение тела (вне зависимости от величины пройденного пути) может находиться как угодно близко к первоначальному положению тела. В случае совпадения конечного и начального положений тела, модуль перемещения будет равен нулю.
7. Почему в механике более важен вектор перемещения тела, чем пройденный им путь?
7. Основной задачей механики является определение положения тела в любой момент времени. Зная вектор перемещения тела мы можем определить координаты тела, т.е. положение тела в любой момент времени, а зная только пройденный путь мы не можем определить координаты тела, т.к. мы не имеем сведений о направлении движения, а можем только судить о длине пройденного пути на данный момент времени.
а. Проекцией точки А на ось PQ (рис. 4) называется основание а перпендикуляра, опущенного из данной точки на данную ось. Та ось, на которую мы проектируем, называется осью проекций.
Ь. Пусть даны две оси и вектор А В, указанные на рис. 5.

Вектор началом которого служит проекция начала и концом - проекция конца данного вектора, называется проекцией вектора А В на ось PQ, Записывается это так;
![]()
Иногда указатель PQ внизу не пишется, это делается в тех случаях, когда кроме PQ нет другой осиг на которую можно было бы проектировать.
с. Теорема I. Величины векторов, лежащих на одной оси, относятся как величины их проекций на любую ось.

Пусть даны оси и векторы, указанные на рис, 6. Из подобия треугольников видно, что длины векторов относятся, как длины их проекций, т. е.
![]()
Так как векторы на чертеже направлены в разные стороны, то величины их имеют различный внак, следовательно,
![]()
Очевидно, величины проекций также имеют различный знак:
![]()
подставляя (2) в (3) в (1), получим
![]()
Меняя знаки на обратные, получим
![]()
Если векторы будут одинаково направлены, то будут одного направления и их проекции; в формулах (2) и (3) знаков минус не будет. Подставляя (2) и (3) в равенство (1), мы сразу получим равенство (4). Итак, теорема доказана для всея случаев.

d. Теорема II. Величина проекции вектора на любую ось равна величине вектора, умножен» ной на косинус угла между осью проекций и осью вектора, Пусть даны оси вектор как указано на рис. 7. Построим вектор одинаково направленный со своей осью и отложенный, например, от точки пересечения осей. Пусть длина его равна единице. Тогда и величина его
![]()
Определение 1. На плоскости параллельной проекцией точки А на ось l называется точка - точка пересечения оси l с прямой, проведенной через точку А параллельно вектору, задающему направление проектирования.
Определение 2. Параллельной проекцией вектора на ось l (на вектор) называется координата вектора, относительно базиса оси l, где точки и - параллельные проекции соответственно точек А и В на ось l (рис. 1).
Согласно определению имеем
Определение 3. если и базис оси l декартов, то есть, то проекция вектора на ось l называется ортогональной (рис. 2).
В пространстве определение 2 проекции вектора на ось остается в силе, только направление проектирования задается двумя неколлинеарными векторами (рис. 3).

Из определения проекции вектора на ось вытекает, что каждая координата вектора есть проекция этого вектора на ось, определяемую соответствующим базисным вектором. При этом направление проектирования задается двумя другими базисными векторами, если проектирование ведется (рассматривается) в пространстве, или другим базисным вектором, если проектирование рассматривается на плоскости (рис. 4).

Теорема 1. Ортогональная проекция вектора на ось l равна произведению модуля вектора на косинус угла между положительным направлением оси l и, т. е.

С другой стороны
Из находим
Подставив АС в равенство (2), получим
Так как числа x и одного знака в обоих рассматриваемых случаях ((рис. 5, а) ; (рис. 5, б) , то из равенства (4) следует
Замечание. В дальнейшем мы будем рассматривать только ортогональную проекцию вектора на ось и поэтому слово «орт» (ортогональная) в обозначении будем опускать.
Приведем ряд формул, которые используются в дальнейшем при решении задач.
а)Проекция вектора на ось.
Если, то ортогональная проекция на вектор согласно формуле (5) имеет вид
в) Расстояние от точки до плоскости.

Пусть б - данная плоскость с нормальным вектором, M - данная точка,
d - расстояние от точки М до плоскости б (рис. 6).
Если N- произвольная точка плоскости б, а и - проекции точек Mи Nна ось, то
- г) Расстояние между скрещивающимися прямыми.

Пусть а и b- данные скрещивающиеся прямые, - перпендикулярный им вектор, А и В - произвольные точки прямых а и b соответственно (рис. 7), и - проекции точек Aи Bна, тогда
д) Расстояние от точки до прямой.
Пусть l - данная прямая с направляющим вектором, M - данная точка,
N - ее проекция на прямую l , тогда - искомое расстояние (рис. 8).
Если А - произвольная точка прямой l , то в прямоугольном треугольнике MNAгипотенуза MAи катет могут быть найдены. Значит,

е) Угол между прямой и плоскостью.

Пусть - направляющий вектор данной прямой l , - нормальный вектор данной плоскости б, - проекция прямой l на плоскость б (рис. 9).
Как известно, угол ц между прямой l и ее проекцией на плоскость б называется углом между прямой и плоскостью. Имеем
Приведем примеры решения метрических задач векторно-координатным методом.
§ 3. Проекции вектора на оси координат1. Нахождение проекций геометрически.
Вектор
- проекция вектора на ось OX
- проекция вектора на ось OY
Определение 1. Проекцией вектора на какую-либо ось координат называется взятое со знаком "плюс" или "минус" число, соответствующее длине отрезка, расположенного между основаниями перпендикуляров, опущенных из начала и конца вектора на ось координат.
Знак проекции определяется так. Если при движении вдоль оси координат происходит перемещение от точки проекции начала вектора к точке проекции конца вектора в положительном направлении оси, то проекция вектора считается положительной. Если же - противоположно оси, то проекция считается отрицательной.

По рисунку видно, что если вектор ориентирован как-то противоположно оси координат, то его проекция на эту ось отрицательна. Если вектор ориентирован как-то в положительном направлении оси координат, то его проекция на эту ось положительна.

Если
вектор перпендикулярен оси координат,
то его проекция на эту ось равна нулю.
Если вектор сонаправлен с осью,
то его проекция на эту ось равна модулю
вектора.
Если вектор противоположно
направлен оси координат, то его
проекция на эту ось по абсолютной
величине равна модулю вектора, взятому
со знаком минус.
2. Наиболее общее определение проекции.

Из прямоугольного треугольника ABD :.
Определение 2. Проекцией вектора на какую-либо ось координат называется число, равное произведению модуля вектора и косинуса угла, образованного вектором с положительным направлением оси координат.

Знак
проекции определяется знаком косинуса
угла, образованного вектором с
положительным направлением оси.
Если угол острый, то косинус
имеет положительный знак, и проекции -
положительны. Для тупых углов косинус
имеет отрицательный знак, поэтому в
таких случаях проекции на ось
отрицательны.![]() -
поэтому для векторов, перпендикулярных
к оси, проекция равна нулю.
-
поэтому для векторов, перпендикулярных
к оси, проекция равна нулю.
В этой статье мы разберемся с проекцией вектора на ось и научимся находить числовую проекцию вектора. Сначала дадим определение проекции вектора на ось, введем обозначения, а также приведем графическую иллюстрацию. После этого озвучим определение числовой проекции вектора на ось, рассмотрим способы ее нахождения и покажем решения нескольких примеров, в которых требуется найти числовую проекцию вектора на ось.
Навигация по странице.
Проекция вектора на ось – определение, обозначение, иллюстрации, пример.
Начнем с общих сведений.
Под осью понимается прямая, для которой указано направление. Таким образом, проекция вектора на ось и проекция вектора на направленную прямую – это одно и то же.
Проекцию вектора на ось можно рассматривать в двух смыслах: геометрическом и алгебраическом. В геометрическом смысле проекция вектора на ось есть вектор, а в алгебраическом – число. Часто это разграничение явно не указывается, а понимается из контекста. Мы же не станем игнорировать это разграничение: будем использовать термин «», когда речь идет о проекции вектора в геометрическом смысле, и термин «», когда речь идет о проекции вектора в алгебраическом смысле (числовой проекции вектора на ось посвящен следующий пункт этой статьи).
Теперь переходим к определению проекции вектора на ось. Для этого не помешает повторить .
Пусть на плоскости или в трехмерном пространстве нам задана ось L и ненулевой вектор . Обозначим проекции точек А и В на прямую L соответственно как А 1 и В 1 и построим вектор . Забегая вперед скажем, что вектор - это проекция вектора на ось L .
Определение.
Проекция вектора на ось – это вектор, началом и концом которого являются соответственно проекции начала и конца заданного вектора.
Проекцию вектора на ось L обозначают как .
Чтобы построить проекцию вектора на ось L , нужно из точек А и В опустить перпендикуляры на направленную прямую L – основания этих перпендикуляров дадут начало и конец искомой проекции .

Приведем пример проекции вектора на ось.
Пусть на плоскости введена прямоугольная система координат Oxy и задана некоторая точка . Изобразим радиус-вектор точки М 1 и построим его проекции на координатные оси Ox и Oy . Очевидно, ими являются векторы с координатами и соответственно.

Часто можно слышать о проекции одного вектора на другой ненулевой вектор или о проекции вектора на направление вектора . В этом случае подразумевается проекция вектора на некоторую ось, направление которой совпадает с направлением вектора (вообще существует бесконечно много осей, направления которых совпадают с направлением вектора ). Проекция вектора на прямую, направление которой определяет вектор , обозначается как .
Отметим, что если угол между векторами и острый, то векторы и сонаправлены. Если угол между векторами и тупой, то векторы и противоположно направлены. Если же вектор нулевой или перпендикулярен вектору , то проекция вектора на прямую, направление которой задает вектор , есть нулевой вектор.
Числовая проекция вектора на ось – определение, обозначение, примеры нахождения.
Числовой характеристикой проекции вектора на ось является числовая проекция этого вектора на данную ось.
Определение.
Числовая проекция вектора на ось – это число, которое равно произведению длины данного вектора на косинус угла между этим вектором и вектором, определяющим направление оси.
Числовую проекцию вектора на ось L обозначают как (без стрелочки сверху), а числовую проекцию вектора на ось, определяемую вектором , - как .
В этих обозначениях определение числовой проекции вектора на прямую, направленную как вектор , примет вид  , где - длина вектора , - угол между векторами и .
, где - длина вектора , - угол между векторами и .
Итак, мы имеем первую формулу для вычисления числовой проекции вектора : . Эта формула применяется, когда известны длина вектора и угол между векторами и . Несомненно, эту формулу можно применять и тогда, когда известны координаты векторов и относительно заданной прямоугольной системы координат, однако в этом случае удобнее использовать другую формулу, которую мы получим ниже.
Пример.
Вычислите числовую проекцию вектора на прямую, направленную как вектор , если длина вектора равна 8 , а угол между векторами и равен .
Решение.
Из условия задачи имеем  . Осталось лишь применить формулу, позволяющую определить требуемую числовую проекцию вектора:
. Осталось лишь применить формулу, позволяющую определить требуемую числовую проекцию вектора:
Ответ:
Нам известно, что  , где – скалярное произведение векторов и . Тогда формула
, где – скалярное произведение векторов и . Тогда формула  , позволяющая найти числовую проекцию вектора на прямую, направленную как вектор , примет вид
, позволяющая найти числовую проекцию вектора на прямую, направленную как вектор , примет вид  . То есть, мы можем сформулировать еще одно определение числовой проекции вектора на ось, которое эквивалентно определению, данному в начале этого пункта.
. То есть, мы можем сформулировать еще одно определение числовой проекции вектора на ось, которое эквивалентно определению, данному в начале этого пункта.
Определение.
Числовая проекция вектора на ось , направление которой совпадает с направлением вектора , - это отношение скалярного произведения векторов и к длине вектора .
Полученную формулу вида удобно применять для нахождения числовой проекции вектора на прямую, направление которой совпадает с направлением вектора , когда известны координаты векторов и . Покажем это при решении примеров.
Пример.
Известно, что вектор задает направление оси L . Найдите числовую проекцию вектора на ось L .
Решение.
Формула в координатной форме имеет вид  , где и . Используем ее для нахождения требуемой числовой проекции вектора на ось L
:
, где и . Используем ее для нахождения требуемой числовой проекции вектора на ось L
:
Ответ:
Пример.
Относительно прямоугольной системы координат Oxyz
в трехмерном пространстве заданы два вектора ![]() и
и ![]() . Найдите числовую проекцию вектора на ось L
, направление которой совпадает с направлением вектора .
. Найдите числовую проекцию вектора на ось L
, направление которой совпадает с направлением вектора .
Решение.
По координатам векторов ![]() и
и ![]() можно вычислить скалярное произведение этих векторов:
можно вычислить скалярное произведение этих векторов:  . Длина вектора по его координатам вычисляется по следующей формуле
. Длина вектора по его координатам вычисляется по следующей формуле ![]() . Тогда формула для определения числовой проекции вектора на ось L
в координатах имеет вид
. Тогда формула для определения числовой проекции вектора на ось L
в координатах имеет вид  .
.
Применим ее:
Ответ:
Теперь давайте получим связь между числовой проекцией вектора на ось L
, направление которой определяет вектор , и длиной проекции вектора на ось L
. Для этого изобразим ось L
, отложим векторы и из точки, лежащей на L
, опустим перпендикуляр из конца вектора на прямую L
и построим проекцию вектора на ось L
. В зависимости от меры угла между векторами и возможны следующие пять вариантов:

В первом случае очевидно, что , следовательно, , тогда  .
.
Во втором случае в отмеченном прямоугольном треугольнике из определения косинуса угла имеем  , следовательно,
, следовательно,  .
.
В третьем случае очевидно, что , а  , следовательно, и
, следовательно, и  .
.
В четвертом случае из определения косинуса угла следует, что  , откуда
, откуда  .
.
В последнем случае , следовательно, , тогда  .
.
Следующее определение числовой проекции вектора на ось объединяет в себе полученные результаты.
Определение.
Числовая проекция вектора на ось L , направленную как вектор , это
Пример.
Длина проекции вектора на ось L , направление которой задает вектор , равна . Чему равна числовая проекция вектора на ось L , если угол между векторами и равен радиан.
-
 Проповеди митрополита Варсонофия
Проповеди митрополита Варсонофия
-
 «Комплексный подход к работе учителя – логопеда и педагога – психолога с детьми, имеющими речевые нарушения Характеристика изменений в
образовательном процессе
«Комплексный подход к работе учителя – логопеда и педагога – психолога с детьми, имеющими речевые нарушения Характеристика изменений в
образовательном процессе
-
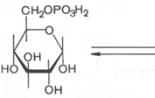 Бескислородное окисление глюкозы включает два этапа
Бескислородное окисление глюкозы включает два этапа
-
 Иисус навин кто он. Иисус сын навин. Вхождение в Землю Обетованную
Иисус навин кто он. Иисус сын навин. Вхождение в Землю Обетованную